Quadratic equations form the cornerstone of algebra, serving as fundamental building blocks in various branches of mathematics and science. Among the plethora of quadratic equations, 4x ^ 2 – 5x – 12 = 0 stands out as a prime example, showcasing the standard form of such equations: ax^2 + bx + c = 0, where a, b, and c are constants, and x represents the variable. This particular equation intrigues mathematicians and scientists alike due to its coefficients and the solutions it yields. In this article by babajitone.com, we’ll delve deep into the methods of solving this equation, analyzing its roots, exploring its significance, and understanding its applications in the real world.

Method of Solution: 4x ^ 2 – 5x – 12 = 0

To solve the quadratic equation 4x ^ 2 – 5x – 12 = 0, several methods can be employed. One common approach is factoring, where we decompose the quadratic expression into two linear expressions and then solve for x. However, this method may not always be applicable, especially for more complex equations.

Another method is completing the square, which involves transforming the equation into a perfect square trinomial and then solving for x. This method is particularly useful for quadratic equations that cannot be easily factored.

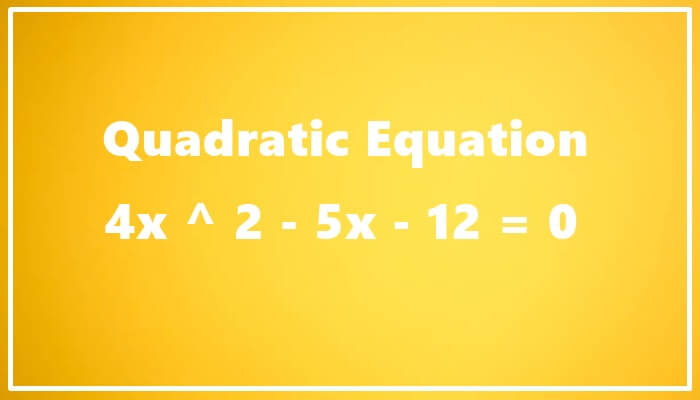
How to Find Roots of Quadratic Equation by Method of Completing the Square?

The method of completing the square involves several steps:

1. Write the equation in the form ax^2 + bx + c = 0.
2. Move the constant term to the other side of the equation.
3. Divide all terms by the coefficient of x^2 to make the leading coefficient 1.
4. Add and subtract the square of half of the coefficient of x.
5. Factor the perfect square trinomial.
6. Take the square root of both sides and solve for x.

By applying these steps to the equation 4x ^ 2 – 5x – 12 = 0, we can find the roots of the equation.

Analyzing the Roots

After applying the method of completing the square, we obtain the roots of the quadratic equation. The roots represent the values of x that satisfy the equation and are crucial in understanding the behavior of the equation.

In the case of 4x^2 – 5x – 12 = 0, the roots can be real or complex, depending on the discriminant (b^2 – 4ac). If the discriminant is positive, the roots are real and distinct; if it is zero, the roots are real and equal; and if it is negative, the roots are complex.

Calculation

By applying the method of completing the square to the equation 4x ^ 2 – 5x – 12 = 0 we find the roots as follows:

1. Move the constant term to the other side: 4x^2 – 5x = 12.
2. Divide all terms by the coefficient of x^2: (4x^2 – 5x) / 4 = 12 / 4.
3. Add and subtract the square of half of the coefficient of x: (4x^2 – 5x + (5/2)^2) – (5/2)^2 = 12 / 4.
4. Factor the perfect square trinomial: (2x – 5/2)^2 = 12 / 4.
5. Take the square root of both sides: 2x – 5/2 = ±√(12 / 4).
6. Solve for x: 2x = 5/2 ± √3, x = (5 ± √3) / 4.

Therefore, the roots of the equation 4x^2 – 5x – 12 = 0 are (5 + √3) / 4 and (5 – √3) / 4.

Significance and Applications

Quadratic equations like 4x ^ 2 – 5x – 12 = 0 have significant importance in various fields, including mathematics, physics, engineering, economics, and computer science. They serve as models for various real-world phenomena and are used extensively in problem-solving and optimization tasks.

In mathematics, quadratic equations are fundamental to understanding polynomial functions and their properties. They provide insights into the behavior of functions and help in graphing and analyzing parabolas.

In physics, quadratic equations are prevalent in mechanics, describing the motion of objects under the influence of forces. They are used to solve problems related to projectile motion, gravitational acceleration, and harmonic motion.

In engineering, quadratic equations find applications in designing structures, analyzing circuits, and optimizing systems. They play a crucial role in areas such as control theory, signal processing, and structural analysis.

In economics, quadratic equations are used to model various relationships, such as cost functions, revenue functions, and profit functions. They help economists analyze market behavior, consumer preferences, and production efficiency.

In computer science, quadratic equations are employed in algorithms and computational methods. They are used in tasks such as root-finding, optimization, and numerical simulation.

Real-World Example

Consider a scenario where a ball is thrown upward with an initial velocity of 20 m/s. The height h (in meters) of the ball above the ground at time t (in seconds) can be modeled by the quadratic equation h = -5t^2 + 20t.

To find the time it takes for the ball to reach its maximum height, we can use the quadratic equation h = -5t^2 + 20t. By finding the vertex of the parabola representing the height-time relationship, we determine the time at which the ball reaches its maximum height.

Using the method of completing the square, we find the time t when the ball reaches its maximum height:

1. Write the equation in the form h = -5t^2 + 20t.
2. Move the constant term to the other side: -5t^2 + 20t = 0.
3. Divide all terms by the coefficient of t^2: (-5t^2 + 20t) / -5 = 0 / -5.
4. Add and subtract the square of half of the coefficient of t: (-5t^2 + 20t + (20/2)^2) – (20/2)^2 = 0 / -5.
5. Factor the perfect square trinomial: -(t – 2)^2 = 0 / -5.
6. Take the square root of both sides: t – 2 = ±√(0 / -5).
7. Solve for t: t = 2 seconds.

Therefore, the ball reaches its maximum height at t = 2 seconds.

Conclusion

Quadratic equations, exemplified by 4x ^ 2 – 5x – 12 = 0, are essential mathematical tools with diverse applications across various fields. By employing methods such as completing the square, we can solve these equations and analyze their roots. Understanding quadratic equations is crucial for comprehending mathematical concepts, solving real-world problems, and advancing scientific knowledge. As we continue to explore the depths of mathematics and its applications, quadratic equations remain a cornerstone of our journey toward discovery and innovation.